4.2. How octree works

4.2. How octree works
	Chapter 4. Octrees

4.2. How octree works

Octree is a tree where each internal (non-leaf) node has eight children. Each node spans a particular space area, expressed as an axis-aligned bounding box (available as Box property of TOctreeNode). Each node also has a chosen middle point inside this box (available as MiddlePoint property of TOctreeNode class). This point defines three planes parallel to the base X, Y and Z planes and crossing this point. Each child of given octree node represents one of the eight space parts that are created by dividing parent space using these three planes.

Each child, in turn, may be either

Another internal node. So it has his own middle point and another eight children. His middle point must be within the space part that his parent node gave him.
Or a leaf, that simply contains actual items that you wanted to store in an octree. What is an “actual item” depends on with want items you want to calculate collisions using this octree.
In our engine we have two octree types:
1. TTriangleOctree that keeps triangles
2. TShapeOctree that keeps VRML shapes. Shape is a pair of TVRMLGeometryNode (remember from Section 3.7, “Geometry nodes features” that these are the only VRML nodes that actually have some geometry visible) and it's State (obtained from traversing VRML graph).

What happens when given item should be included in more than one children? That is, item is contained in space part of more than one children?

Simple solution is to put this item inside all children where it should be. This means that we could waste a lot of memory if given item should be present in many leaf nodes, but this problem can be somewhat cured by just keeping an array of octree items for the whole octree (like TTriangleOctree.Triangles or TShapeOctree.ShapesList) and keeping only indexes to this array in octree leafs (ItemsIndices property of TOctreeNode).
Another possible solution is to keep such problematic item only in the list of items of internal node, instead of putting it inside children nodes. But each octree node has eight children, and given item can be contained for example only in two of eight children. In this case our collision checking routines would always have to consider this item, while in fact they should consider it only for a 2/8 part of the space.
That's why my engine doesn't use this approach. Note that some hybrid approach could be possible here, for example keep the item if it spans more than 4 children nodes and put it inside children otherwise. This idea remains to be implemented one day... For now our collision checking is fast enough for all purposes when it's needed in real-time games.

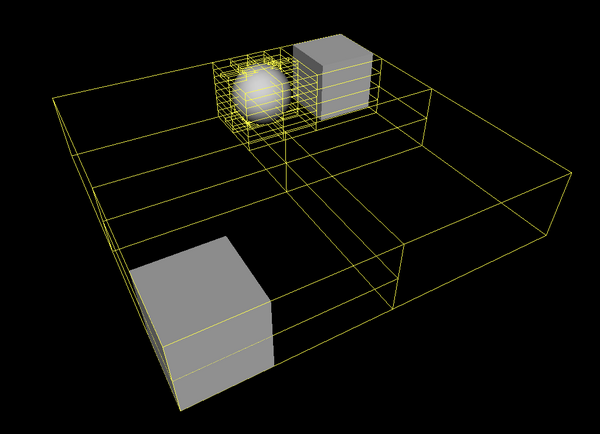
Example below shows an octree constructed by our engine. The sample scene contains two boxes and a sphere. On the screenshot yellow bounding boxes indicate every internal node and every non-empty leaf. Whole scene is contained within root node of the tree, so the largest yellow bounding box corresponds also to the bounding box of the scene. The “lonely” box (in the foreground) is placed within the two direct children on the root tree node. Left and right quarter on the image contain only empty children leaves of root node, so their bounding boxes are not shown. Finally, the interesting things happen in the quarter with a box and a sphere. Sphere has many triangles, so a detailed octree is constructed around it. Also the sphere caused a little more detailed octree around the near box.

#VRML V2.0 utf8

Viewpoint  {
  position -10.642 8.193 -5.614
  orientation -0.195 -0.921 -0.336 2.158
}

Transform {
  translation 4 0 1.25
  children Shape {
    appearance DEF ALit Appearance { material Material { } }
    geometry Sphere { }
  }
}

Transform {
  translation 4 0 4
  children Shape {
    appearance USE ALit
    geometry Box { }
  }
}

Transform {
  translation -4 0 -4
  children Shape {
    appearance USE ALit
    geometry Box { }
  }
}

Figure 4.1. A sample octree constructed for a scene with two boxes and a sphere

You can view octree like this using view3dscene. Just turn on the menu option “View” -> “Show whole octree”. There are also menu commands to investigate octree nodes only at the particular depth.

4.2.1. Checking for collisions using the octree

Let's assume that you have some reference object (like a sphere or a ray or a line segment mentioned in the first section) that you want to check for collisions with all items contained in the octree. You start from the root node — all items, which means “all potential colliders”, are there. You check with which children of this node your object could possibly collide. Different object types will require various approaches here. In general, this comes down to checking for collision between children nodes' boxes and your reference object. For example:

For a sphere, you check which child node contains the sphere center. Then you check with which planes (of the three dividing planes of this node) the sphere collides. This determines all the children that the sphere can collide with.
Above approach is not as accurate as it could be — since it effectively checks the collision of the bounding box of the sphere with children boxes. To make it more accurate you can check whether the middle point of given node is within the sphere. But it's not certain whether this additional check will make your collision detection faster (because we will descend into less children nodes) or slower (because we spend time on the additional check). In practice, this depends on how large spheres you will check for collision — for small (small in comparison to the world) spheres, this additional check will seldom eliminate any child and probably will be worthless.
For a ray: determine child node where ray start is. Then check for collision between this ray and three base planes crossing node's middle point. This will let you determine into which children nodes the ray enters. Similar approach could be taken for the line segment.
For a frustum: first note that our engine stores frustum as a 6 plane equations.
The basic approach here is to employ the method of checking for collision between a plane and a box. To determine collision of a box with a plane you can check 8 box corners on which side of the plane they are (simply by checking expression similar to the plane equation, Ax + Bx + Cz + D >= 0). If all points are on the same side of the plane (and no point lies precisely on the plane) then there is no collision. This also tells your on which size of the plane the box is located, in case there is no collision.
In our engine, frustum planes are correctly oriented, so the answer to the question “on which size of the plane” a box is located is meaningful to us. To check for collision of frustum with a node, we check 6 frustum planes for collision with this node's box. If box is on the inside side of every plane, this means that the box is completely inside the frustum. Otherwise, if the box is on the outside side of at least one plane, then the box is completely outside of the frustum. Otherwise (which means that box collides with at least one plane, and it's not outside any plane) we don't really know.
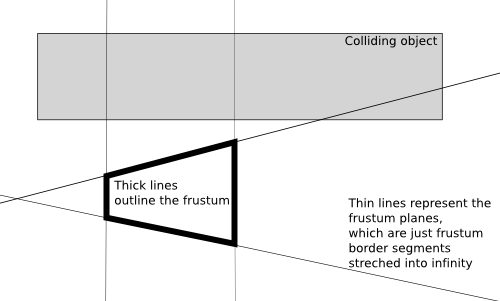
In the last case, we're pretty certain that the box collides somehow with the frustum, so we assume this. In case of error, nothing terrible will happen: our collision checking routine using octree will just work a little slower than possible, but it will still be 100% correct. In practice, in almost all cases our assumption will be true, although some nasty cases are indeed possible. You can see an example of such case below. This is a side view showing a frustum and a box. You can see that the box collides with 3 planes and is considered to be on the inside of the 4th plane (the one at the bottom). You can easily extend this image to 3D and imagine the remaining 2 frustum planes in such way that they will intersect the box.

Figure 4.2. A nasty case when a box is considered to be colliding with a frustum, but in fact it's outside of the frustum

Once you can check with which octree node's children your object collides, you just apply this process recursively. That is, for each internal node you determine which of it's children may collide with your reference object, and recursively check for collisions inside these children. For each leaf node, you just sequentially check all it's items for collision. For example, in case of a triangle octree, in the leafs you will check for collision between triangles and your reference object.

What's the time of this collision checking algorithm? Like with all tree structures, the idea is that the time should be logarithmic. But actually we don't use any advanced techniques that could ensure that our octree is really balanced. And the fact that items that are put inside more than one children are effectively multiplied in the octree doesn't help either. However octrees of real-world models are enough balanced (and multiplication is small enough) to make collision checking using octrees “logarithmic (i.e. fast) in practice”.

Some more notes about collision checking using an octree:

Sometimes all you need is the information that “some collision occurred” (for example that's enough for shadow detection). Sometimes you want to get the closest collision point (for example, closest to the ray start, for ray-tracing). The first case can obviously be optimized to finish whole algorithm as soon as any collision is found. In the second case you must always check all items when you process a leaf node (because the items in leaf nodes are not ordered in any way). But when processing internal nodes it can still be optimized to not enter some children nodes if collision in earlier child node was found (in cases when we know that every possible collision in one child node must be closer to ray start than every possible collision in other node).
As was mentioned earlier, if an octree item fits into more than one child of given node, we put it inside every matching children node, thus duplicating information about this item in many leafs. But this means that we can lose some speed. We can be fooled into checking more than once for collision between our reference object (like a ray) with the same item, but placed within a different leaf.
This is not so terribly bad, since we are talking here about tests like checking for collision between a single ray and a single triangle. So this test is anyway quite fast operation, in constant time. But still it requires a couple of floating point operations, and it's called very often by our algorithm, so we want to optimize it.
The solution is called the mailboxes. Each octree item gets a mailbox. Each reference object (like a ray) gets a unique tag. Before we check for collision between our reference object and an octree item, we check whether the mailbox has the information about the collision test result for this object tag. If yes, then we obtain the collision test result from the mailbox. Otherwise, we perform normal (more time-consuming) test and we store the test result along with the object tag within the mailbox. This way each item will be tested for collision with reference object only once. Next time we will just use the mailbox.
This is possible to implement thanks to the fact that we keep indexes to items in octree nodes, and the actual items are kept in an array for a whole octree. So we can naturally place our mailboxes in this array.

4.2.2. Constructing octree

A simple algorithm starts with an empty tree, containing one leaf node with no items. Then we add our items (triangles, VRML shapes etc.) to the octree keeping an assertion that no leaf can have more than some specified number of items (LeafCapacity property of TOctree class). When we see that adding another item to some leaf would break this assertion, we convert the leaf to an internal node with eight children, and we add items (previous leaf items and the new item that we're trying to add) to newly created children. Of course, each children gets only the items that are within its space part.

Note that this algorithm doesn't guarantee in any way that a tree is balanced. And we want the tree to be balanced, otherwise checking for collisions using this tree will be as slow (or even slower) than just sequentially checking collision with all items. However, for most real-world models, the items are spread more-or-less evenly across the scene, so in practice our tree is more-or-less balanced. To prevent the pathological cases that could result in extremely deep octrees we can add a simple limit on the allowed depth of the tree (MaxDepth property of TOctree class). When a leaf reaches MaxDepth, we will not split it to an internal node anymore, no matter how many items does it contain. So the assertion becomes “leafs on depth < MaxDepth must have at most LeafCapacity items”. This way the nasty cases are somewhat bounded — our collision checking using tree cannot be much slower than just sequentially checking for collision with all contained items.

There is a question how to calculate middle point of each node. The simple and most common approach is just to calculate it as an actual middle point of the node's box. Root tree node gets a box equal to the bounding box of our scene. But you could plug here other techniques. The basic idea is that the tree should be balanced, so ideally the middle point should divide the node's box into eight parts with equal number of triangles inside.

For some purposes it's helpful to keep in each internal node a list of all items contained within it's children. This eats more memory, but may allow in some cases to terminate the collision checking operation faster. For example, when we want to check which octree items are inside a camera frustum, we often find ourselves in a situation when we know that some octree node is completely contained within the frustum. If we have all the items' indexes easily accessible within this internal node, we can avoid having to traverse all children nodes under this node. This is used by TShapeOctree in our engine.


Chapter 4. Octrees		4.3. Octrees for dynamic worlds